
ERRORS & THEIR MEASUREMENTS
Errors and their Adjustments
Source of Errors
Errors in surveying may arise from
three main sources:
Instrumental: Surveying error may
arise due to imperfection or faulty adjustment of the instrument with which
measurement is being taken. For example, a tape may be too long or an angle
measuring instrument may be out of adjustment. Such errors are known as
instrumental errors.
Personal: Error may also arise
due to wanting of perfection of human sight in observing and of touch in
manipulating instruments. For example, an error may be there in taking the
level reading or reading and angle on the circle of a theodolite. Such errors
are known as personal errors.
Natural: Error in surveying
may also be due to variations in natural phenomena such as temperature,
humidity, gravity, wind, refraction and magnetic declination. If they are not
properly observed while taking measurements, the results will be incorrect. For
example, a tape maybe 20 meters at 200C but its length will change if the field
temperature is different.
Types of Surveying Errors
Ordinary errors in surveying met within
all classes of survey work may be classified as:
Mistakes
Accidental errors
Systematic or cumulative errors
Compensating errors
Mistakes: Mistakes are errors
that arise from inattention, inexperience, carelessness and poor judgment or
confusion in the mind of the observer. They do not follow any mathematical rule
(law of probability) and may be large or small, positive or negative. They
cannot be measured.
Accidental Errors: Surveying
errors can occur due to unavoidable circumstances like variations in
atmospheric conditions which are entirely beyond the control of the observer.
Errors in surveying due to imperfection in measuring instruments and even
imperfection of eyesight fall in this category. They may be positive and may
change sign. They cannot be accounted for.
Systematic or
Cumulative Errors: A systematic or cumulative error is an error that, under the
same conditions, will always be of the same size and sign. A systematic error
always follows some definite mathematical or physical law and correction can be
determined and applied. Their effect is, therefore, cumulative. For example, if
a tape is P cm short and if it is stretched N times, the total error in the
measurement of the length will be P´N cm.
The systematic errors may arise due to
(i) variations of temperature, humidity, pressure, current velocity, curvature,
refraction, etc. and (ii) faulty setting or improper leveling of any instrument
and personal vision of an individual. The following are the examples:
Faulty alignment of a line
An instrument is not leveled properly
An instrument is not adjusted properly
Compensating
Errors: This
type of surveying error tends to occur in both directions, i.e. the error may
sometimes tend to be positive and sometimes negative thereby compensating each
other. They tend sometimes in on direction and sometimes in the other, i.e.
they are equally likely to make the apparent result large or small. The
following are a few examples:
The discrepancy between chain and tape
measurements when both are used simultaneously.
Inaccuracy in marking chain lengths on
the ground.
Inaccurate centering.
Inaccurate bisection of an object.
Propagation of Errors
Measurements are used for the
calculation of different parameters. As the measurements are fraught with
errors, it is important to know how these errors combine in various
mathematical operations.
Error Propagation in
a sum or difference of measurements:
When two or more quantities are added
or subtracted, the error in result (Es) is the square root of the sum of the
square of the errors (e1, e2, .....) of the individual quantity i.e.,

Error Propagation in
a product of measurements:
When two or more quantities are
multiplied, the error in result (Eproduct) is the square root of the
sum of the square of the fractional errors of the individual quantity. Thus
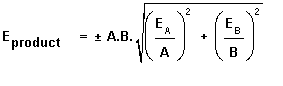
where EA and EB are
errors in observed values of A and B respectively.
For example: A rectangle is
measured 160.881 ± 0.026 cm long and 75.007 ± 0.001 cm wide. The
error in its area (12,067 cm2) is
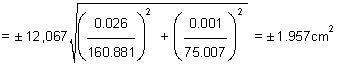
Error Propagation in
a division of measurements:
When two or more quantities are
divided, the error in the result is the square root of the sum of the square of
the fractional errors in the individual quantity.
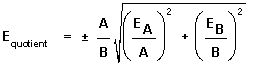
For example: If the area of a rectangular plot is somehow known to be 49,650 ± 10 m2 and the width dimension measured several times found to be 175.66 ± 0.46 m, the calculated length dimension is
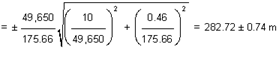


No comments added yet!